Are you a researcher in quantum or classical optimization algorithms?
A new paper from the Quantum Optimization Working Group invites you to test your algorithms on any of the 10 optimization benchmarking problems in the “intractable decathlon,” and submit your results to the open-source Quantum Optimization Benchmarking Library (QOBLIB).
Your contributions — whether quantum or classical — will help to advance the state of the art in optimization algorithms research, and will bring us closer to achieving quantum advantage in optimization.
How will we achieve quantum advantage in optimization? By working together. What does quantum advantage in optimization look like? That’s a longer story.
Last year, the Quantum Optimization Working Group published a white paper in Nature Reviews Physics on the effort to define and discover quantum advantage in optimization. This year, we’re taking that work even further with a new paper detailing what we call the intractable decathlon — ten optimization problem classes designed to help researchers test the limits of state-of-the-art quantum and classical methods. The optimization problems described in this paper also form the basis of the new Quantum Optimization Benchmarking Library (QOBLIB), an open-source repository that researchers can use to submit, track, and compare their benchmarking results. Now, we need your contributions.
Combinatorial optimization is a field of mathematics where our task is to find the best solution to a problem from a discrete set of possible solutions. We use optimization techniques to tackle a wide array of valuable problems across industries and scientific disciplines. However, for many real-world optimization problems, it is still very hard to find provably optimal solutions. That’s why, as we explained in our previous blog on this topic, many of the most effective and widely used quantum and classical optimization algorithms are heuristics — methods that use “rules of thumb,” often based on a deep intuitive understanding of the subject at hand, to efficiently solve complex problems.
By definition, heuristic algorithms cannot offer a priori performance guarantees, meaning it usually isn’t possible to determine in advance which problems they solve well. They’re often great at producing solutions that are “good enough” for practical purposes, but we must test them extensively on real quantum hardware with challenging, practically relevant problems if we want to identify cases of quantum advantage.
With the new Quantum Optimization Benchmarking Library (QOBLIB), we’ve created a centralized resource and testing ground where optimization researchers can work together to assess and advance both quantum and classical optimization methods. There are too many problems and methods for any one researcher or research organization to do this work alone. That’s why we’ve built QOBLIB to leverage the combined expertise of the Quantum Optimization Working Group and the broader optimization research community in pushing the field forward.
The Quantum Optimization Working Group is one of five quantum working groups launched by IBM® and its collaborators to help spur quantum algorithmic development in domains with strong potential to deliver valuable quantum advantages. The new optimization benchmarking paper was written by researchers from more than a dozen member organizations, including Zuse Institute Berlin, Technische Universität Berlin, Purdue University, National University of Singapore, E.ON Digital Technology GmbH, Kipu Quantum GmbH, Forschungszentrum Jülich (the Jülich Research Center), University of Southern California, IBM Quantum®, and more.
The benchmarking problems in the QOBLIB are model-, algorithm-, and hardware-agnostic, meaning you can try your hand at solving them with any quantum or classical optimization technique, deployed on any kind of quantum or classical compute hardware. By exploring these problems with a variety of optimization algorithms and submitting solutions to the open-source, publicly accessible QOBLIB repository, we believe our community can accelerate progress towards discovering practically relevant quantum advantages in combinatorial optimization. However, that will happen only if real researchers join the effort. If you’re a researcher or practitioner who’s ever done work on optimization algorithms, that means you.
The role of benchmarking in the search for quantum advantage
What is the goal of benchmarking in quantum computing and computer science more broadly? Is it to determine better ways of running a fixed algorithm for a fixed problem on a particular platform or system? Is it to identify better strategies for improving particular algorithms, identifying their bottlenecks, and understanding how they scale? Is it to find the best known method — whether quantum or classical — for tackling a particular application?
Systems and algorithms benchmarking can be quite valuable even when they are limited to a specific modeling approach for a problem or problem-solving method, i.e., when they are model- or algorithm-dependent. Applications benchmarking must be model-independent, and in the search for quantum advantage, it’s applications benchmarking that is most essential. Ultimately, we can only demonstrate advantage if our benchmarking allows for all possible approaches to formulating and solving a problem.
Over the years, the research community has done some excellent work in optimization benchmarking. However, this prior work tends to be model-dependent, as it has mostly centered on system and algorithm benchmarking. One of the primary goals behind our new paper is to make up for the general lack of model-independent benchmarking for optimization applications. Developing these model-agnostic benchmarks is certainly more challenging, due to the enormous diversity and complexity that exists in optimization problem classes and their corresponding solution methods, but it is a challenge we must overcome in the pursuit of quantum advantage.
Claims of quantum advantage in any application domain must meet two essential criteria: First, they must concern problems which are truly difficult for all known classical methods. If classical computers can deliver good enough solutions with reasonable time and cost, then there is no point in using quantum computers. Second, they must show that quantum algorithms and quantum hardware can solve the problem more efficiently, more accurately, or at lower cost than all known classical alternatives.
As a rule, finding optimization problems that meet both criteria is quite challenging. Unsolved optimization problems of real business and scientific relevance are rarely published. Researchers tend to discard these seemingly unsolvable problems, replacing them with simplifications whose solutions may be "good enough” for some practical use cases. However, simplification often comes at the cost of quality. If we can solve more complex problems with less reliance on simplifications, we can increase the impact of optimization in practice.
We believe our intractable decathlon is the first collection of scientifically and practically interesting optimization problems that become difficult for state-of-the-art optimization solvers at relatively small problem sizes. The problems are also distinguished by their suitability for exploration on near-term quantum devices which, despite their growing capabilities, are still limited in terms of qubit count and the length of the quantum circuits they can run. These may not necessarily be the problems that will deliver quantum advantage in combinatorial optimization. However, they do give a strong indication of areas where we believe quantum advantage could be found, and we provide clear, well-defined metrics to facilitate the search for advantage and enable fair comparisons between all manner of quantum and classical methods.
Exploring the intractable decathlon
Each problem class detailed in our new optimization benchmarking paper is presented with a brief summary of useful background information, a formal problem statement, a description of the specific problem instances provided for exploration in the open-source Quantum Optimization Benchmarking Library, and classical baseline results to give researchers a running start and facilitate comparisons between quantum and classical methods. We also include quantum baseline results for some of the problems. Now, we’re looking for contributions from the optimization community. If you’re a researcher or practitioner who’s ever done work on optimization algorithms — that means you.
In the QOBLIB repository, we provide problem instances of increasing size and complexity for each of the problem classes — including classically challenging problem instances for all classes — allowing us to track algorithmic and hardware progress toward quantum advantage. We also offer a submission template with clear metrics to enable fair comparisons between different quantum and classical methods. The selected metrics include the achieved solution quality, the total wall clock time, and all computational resources used — both classical and quantum.
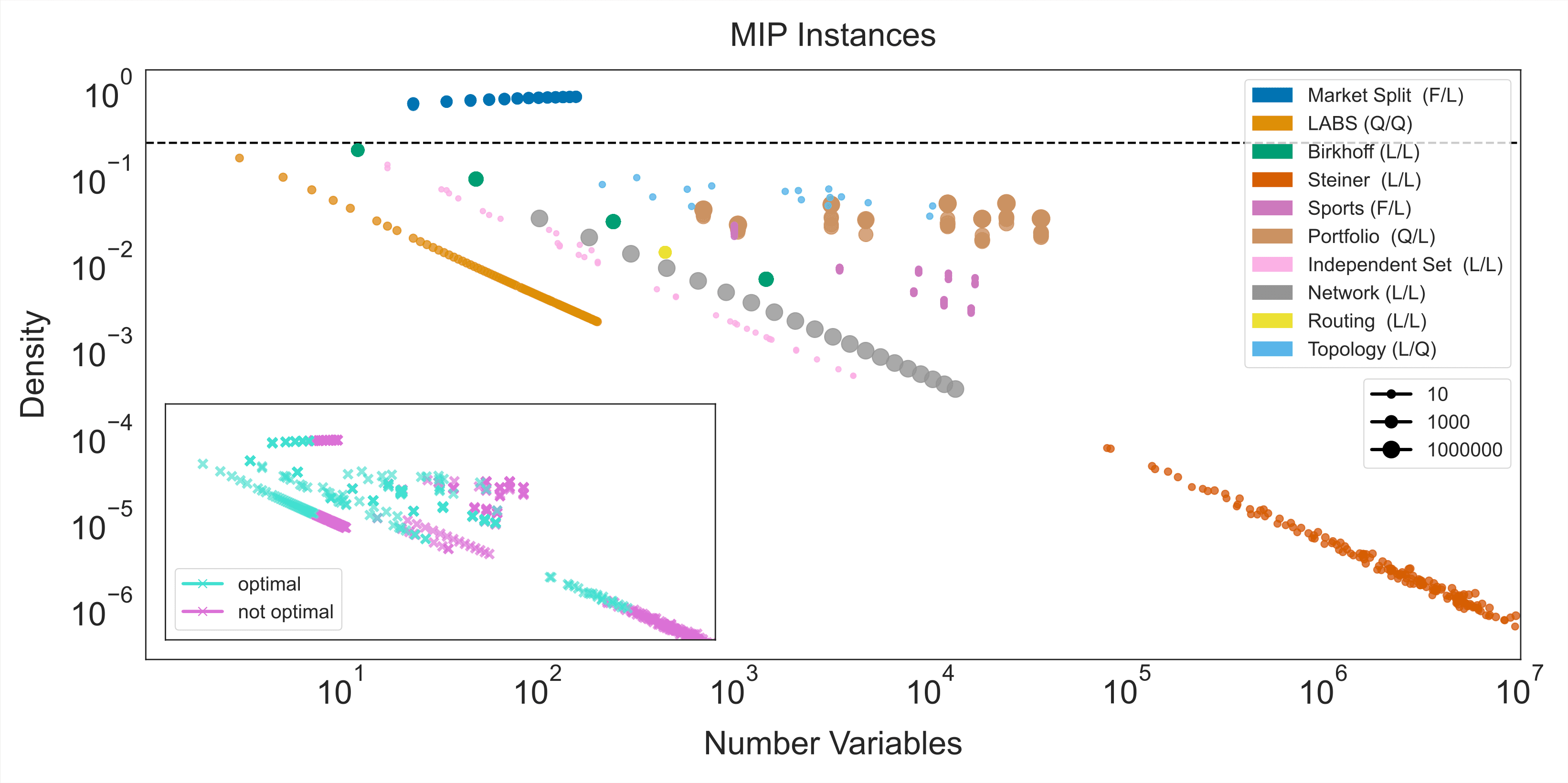
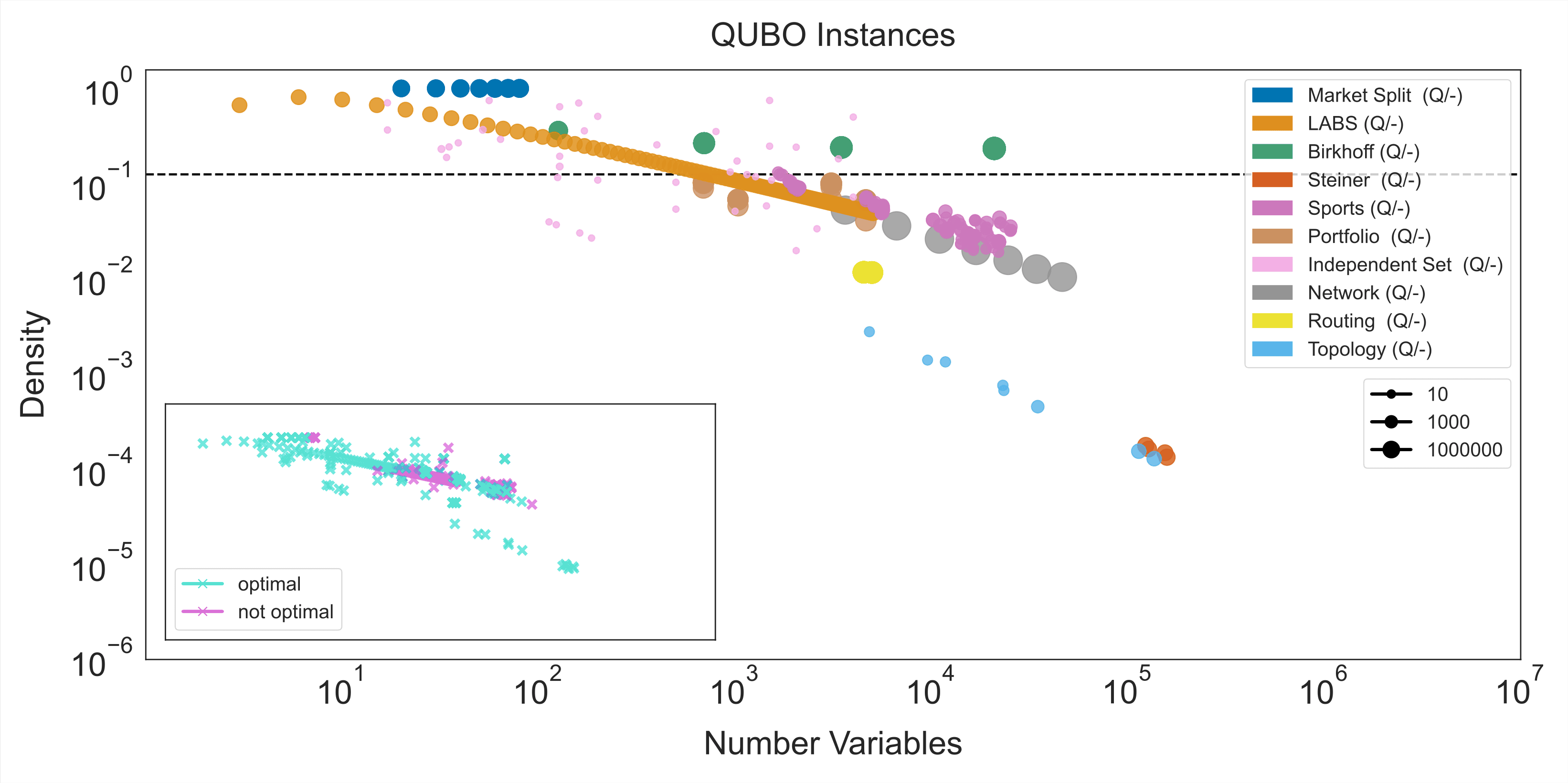
The repository provides access to reference models — both mixed-integer programming (MIP) and quadratic unconstrained binary optimization (QUBO) — which researchers can use in combination with the classical baseline results to analyze the latest quantum algorithms. MIP and QUBO are two different ways of formulating optimization problems — with the MIP formulation often serving as a basic entry point for classical researchers, and QUBO filling the same role for quantum researchers.
Ultimately, we can only demonstrate quantum advantage if we allow researchers to tackle problems in arbitrary ways, and if we do not limit ourselves to particular types of modeling. MIP and QUBO are merely examples of how we can formulate problems, and we make no claims whatsoever about their optimality. Instead, we present them as starting points that researchers can explore and potentially use as inspiration for developing entirely new formulations that may be more amenable to quantum processing, or which may even enable better classical solutions.
In the figures below, you can see how the MIP and QUBO reference models for each problem class change in density as the number of variables increases. It is interesting to note how the process of mapping MIP to QUBO formulations alters the picture. In many cases, this mapping leads to increases in the number of variables, the problem density, and the range of coefficients — all of which contribute to increased model complexity. You can think of these figures as maps of the intractable decathlon, helping you navigate the landscape of problem instances and find the best place to get started.
Ready, set, benchmark!
The potential for quantum advantage in the field of optimization is very real, and with the ten problem classes we’ve presented in our intractable decathlon, we are taking important steps towards realizing that potential. However, this journey is just beginning, and there is such a tremendous variety of problems and algorithms to explore, we know that no individual and no institution can complete it on their own. We will only achieve quantum advantage in optimization if we work together.
If you’re an expert in quantum or classical optimization algorithms, then we need people like you — yes, you! — to join the community effort to test and analyze the performance of quantum and classical optimization methods
Full workflow examples of solving optimization problems on a quantum computer are showcased in IBM Quantum Platform tutorials on QAOA, Advanced techniques for QAOA and Pauli Correlation Encoding for Maxcut. Dive into QAOA for a gentle introduction or check out Advanced techniques for QAOA and Pauli Correlation Encoding for Maxcut for more advanced techniques to get the best performance in hardware experiments.
Working together, we can drive the field of mathematical optimization to a new era in computation, and help the world solve valuable problems beyond the reach of classical methods alone. Are you ready to make your contribution? Read the paper and explore the open-source QOBLIB repository to get started! 🚀




